На фоне слухов о значительно большем «iPhone Math» разработчик Instapaper Марко Армент провел время, разрабатывая некоторые предположения и несколько макетов, показывающих, как Apple могла бы создать iPhone с диагональю почти 5 дюймов, не нарушая существующую экосистему приложений.
Недавно нашумевший «iPhone Math» или, скорее всего, «iPhone Plus» с большим экраном возможен как дополнительная модель (а не замена) наряду с 4-дюймовым iPhone. И весьма вероятно, что у него будет экран 4,94 дюйма с соотношением сторон 16:9.
Теорию легко понять: выполните вычисления Джона Грубера для предсказания Mini в обратном порядке. iPad Mini использует экраны плотностью iPhone 3GS с разрешением iPad. Что, если бы iPhone Plus использовал экраны Retina iPad с разрешением iPhone 5, сохраняя остальную часть дизайна в стиле iPhone 5?
В сценарии, предложенном Арментом, экран с разрешением 1136×640, соответствующий разрешению iPhone 5, но увеличенный до плотности Retina iPad 264 пикселя на дюйм, имел бы диагональ 4,94 дюйма.
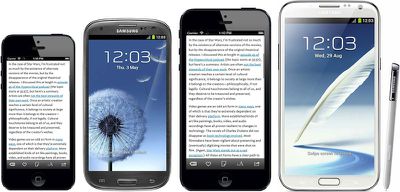
Слева направо: iPhone 5, Galaxy S III, «iPhone Plus», Galaxy Note II
Армент отмечает, что такой iPhone Plus, сохраняя те же пропорции, что и iPhone 5, но с большим экраном, был бы по размеру между Galaxy S III и Galaxy Note II, но Apple, вероятно, смогла бы немного уменьшить нижнюю и верхнюю рамки устройства, чтобы приблизить его к общему размеру Galaxy S III.
При плотности пикселей 264 ppi, как у iPad, Apple может столкнуться с трудностями при позиционировании iPhone Plus как устройства Retina, учитывая, что телефон обычно держат ближе к глазу, чем планшет. Однако некоторые пользователи могут предпочесть возможность иметь больший экран, обеспечивающий большую гибкость, например, возможность увеличивать текст дальше или видеть мелкий текст, удерживая устройство дальше от глаз.
Армент предлагает несколько других макетов, показывающих, как выглядела бы линейка устройств Apple iOS с более крупным iPhone, а также как пользователи могли бы использовать меньшие размеры шрифтов на большом экране для отображения большего количества текста.